Toán 12 đường tiệm cận: Lý thuyết kèm bài tập trắc nghiệm

Tác giả Cô Hiền Trần 14:23 01/12/2023 29,681 Tag Lớp 12

Khi học về đại số trong chương trình toán 12 kiến thức về đường tiệm cận là kiến thức cơ bản, quan trọng và không thể bỏ lỡ. Do đó, các câu hỏi về dạng toán này có thể xuất hiện trong các đề thi THPTQG. Cùng VUIHOC ôn lại lý thuyết và luyện tập các dạng bài nhé!

Toán 12 đường tiệm cận: Lý thuyết kèm bài tập trắc nghiệm

Mục lục bài viết

Mục lục bài viết x

1. Lý thuyết đường tiệm cận - Toán 12

1.1. Đường tiệm cận ngang

Ta sẽ có: đường thẳng y = y0 được gọi là đường tiệm cận ngang (tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $\lim_{x \rightarrow + \infty } f(x) = Y_{0}$

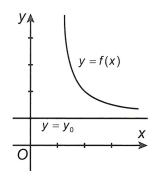
Toán 12 Đường tiệm cận ngang

1.2. Đường tiệm cận đứng

Ta có: đường thẳng x = x0 được gọi là đường tiệm cận đứng (tiệm cận đứng) của đồ thị hàm số y = f(x), nếu ít nhất một trong các điều kiện sau được thỏa mãn:

$\lim_{x \rightarrow x_{0}-} f(x) = + \infty , \lim_{x \rightarrow x_{0}+} f(x) = + \infty$

$\lim_{x \rightarrow x_{0}-} f(x) = - \infty , \lim_{x \rightarrow x_{0}+} f(x) = - \infty$

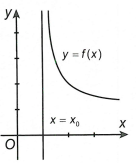
Toán 12 đường tiệm cận đứng

2. Các dạng toán 12 bài 4 đường tiệm cận kèm bài tập trắc nghiệm dễ hiểu nhất

2.1. Dựa vào định nghĩa để xác định các đường tiệm cận

Ví dụ: Các đường tiệm cận $\frac{2x - 1}{x-1}$ là hàm số tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng:

A. 3 (đvdt)

B. 1 (đvdt)

C. 2 (đvdt)

D. 4 (đvdt)

Giải:

Chọn C

Tập xác định D = ℝ \{1}

Đường tiệm cận ngang y=2 và tiệm cận đứng x=1.

Suy ra hình chữ nhật tạo bởi hai đường tiệm cận và hai trục tọa độ sẽ có các kích thước là 1 và 2 nên có diện tích S = 1․2 = 2 (đvdt)

Ví dụ 2: Cho các đường tiệm cận của đường cong (D): $\frac{6x + 1 - \sqrt{x^{2}- 2}}{x-5}$ và cắt trục tung tạo thành một đa giác (H). Mệnh đề nào dưới đây đúng?

A. (H) diện tích một hình chữ nhật bằng 10

B. (H) diện tích một hình vuông bằng 25

C. (H) diện tích của một hình vuông bằng 4

D. (H) diện tích một hình chữ nhật bằng 8

Giải:

Chọn A

Tập xác định $(- \infty , -\sqrt{2}) \cup \left [ \sqrt{2}; +\infty \right ])$ \ {5}

Ta có $\lim_{x\rightarrow x+} = \lim_{x\rightarrow x+} \frac{6x+1- \sqrt{x^{2}-2}}{x-5}$ ⇒ y = 5 => tiệm cận ngang của (D)

$\lim_{x\rightarrow -\infty } = \lim_{x\rightarrow -\infty } \frac{6x+1- \sqrt{x^{2}-2}}{x-5}$ ⇒ y = 7 => tiệm cận ngang của (D)

$\lim_{x\rightarrow 5^{+} } = +\infty , \lim_{x\rightarrow 5^{-} } = -\infty$ ⇒ x = 5 là tiệm cận đứng của (D)

Vậy đồ thị có ba đường tiệm cận: y = 7; y = 5; x = 5 cùng với trục tung tạo thành hình có diện tích hai nhân 5 nên có diện tích bằng 10.

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA

Khóa học online ĐẦU TIÊN VÀ DUY NHẤT:

⭐ Xây dựng lộ trình học từ mất gốc đến 27+

⭐ Chọn thầy cô, lớp, môn học theo sở thích

⭐ Tương tác trực tiếp hai chiều cùng thầy cô

⭐ Học đi học lại đến khi nào hiểu bài thì thôi

⭐ Rèn tips tricks giúp tăng tốc thời gian làm đề

⭐ Tặng full bộ tài liệu độc quyền trong quá trình học tập

Đăng ký học thử miễn phí ngay!!

2.2. Hàm số phân thức: tiệm cận của đồ thị

Phương pháp giải:

Cho hàm số: $y = \frac{ax + b}{cx + d}$

Để tồn tại các đường tiệm cận của đồ thị hàm số $y = \frac{ax + b}{cx + d}$ thì c ≠ 0 và ad – bc ≠ 0

Khi đó, ta có:

+ Tiệm cận đứng $x = \frac{-d}{c}$

+ Tiệm cận ngang $x = \frac{a}{c}$

Ví dụ 1: Giá trị của tham số thực k để đồ thị hàm số $y= \frac{(2m+1) x+1}{x-m}$ có đường tiệm cận ngang y = 3 là:

A. k = 1

B. k = 0

C. k = 2

D. k = 3

Giải

Chọn C

Điều kiện để có tiệm cần là:

– k(2k – 1) – 1 ≠ 0

⇔ 2k2 – k + 1 ≠ 0

⇒ ∀ x ∈ ℝ

Phương trình đường tiệm cận ngang là y = 2k – 1 nên có 2k – 1 = 3 ⇔ k = 2

Ví dụ 2: Tìm tập hợp giá trị thực của m để đồ thị 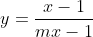$y= \frac{x-1}{mx-1}$ có đường tiệm cận đứng là:

A. ℝ

B. ℝ \{0}

C. ℝ \{1}

D. ℝ \{0; 1}

Giải

Chọn D

Điều kiện để đồ thị hàm số có tiệm cận là m0 và +1-m0 m0 và m1

2.3. Dạng tiệm cận đồ thị của hàm số phân thức hữu tỉ

Dạng 3: Hàm số phân thức hữu tỉ và tiệm cận

Phương pháp giải:

– Đồ thị hàm số $y= \frac{A}{f(x)}$ có tiệm cận với A là số thực khác 0 và f(x) là đa thức bậc n > 0

– Đồ thị hàm số $y= \frac{A}{f(x)}$ luôn có tiệm cận ngang y = 0

– Đường thẳng x = x0 là tiệm cận đứng của đồ thị hàm số $y= \frac{A}{f(x)}$ khi và chỉ khi x0 là nghiệm của f(x) hay f(x0) = 0

– Tiệm cận của đồ thị hàm số $y= \frac{f(x)}{g(x)}$ với f(x), g(x) là các đa thức bậc khác 0

– Điều kiện để đồ thị hàm số $y= \frac{f(x)}{g(x)}$ có tiệm cận ngang là bậc f(x) ≤ bậc g(x)

– Điều kiện để đường thẳng x = x0 là tiệm cận đứng của đồ thị hàm số $y= \frac{f(x)}{g(x)}$ là x0 là nghiệm của g(x)

Ví dụ 1: Tìm mọi giá trị thực tham số m thỏa mãn điều kiện đồ thị hàm số $y= \frac{mx^{2} -2x+1}{2x+1}$ có tiệm cận đứng:

A. m = 8

B. m = 0

C. m ≠ 4

D. m ≠ -8

Giải

Chọn D

Tập xác định D= R \ {-12}

Đặt g(x) = mx2 – 2x + 1

Để đồ thị hàm số có tiệm cận đứng thì $x= -\frac {1}{2}$ không là nghiệm của g(x)

$\Leftrightarrow g (\frac{-1}{2}) \neq \Leftrightarrow \frac{m}{4}+2 \neq 0 \Leftrightarrow m \neq -8$

Ví dụ 2: Biết đồ thị hàm số $y= \frac{x-1}{x^{2} -2mx+n+6}$ (m, n là tham số) nhận đường thẳng x = 1 là tiệm cận đứng, giá trị của m + n bằng

A. 6

B. 10

C. -4

D. -7

Giải

Chọn C

Điều kiện: x2 – 2mx + n + 6 ≠ 0

Đặt g(x) = x2 – 2mx + n + 6

Đường thẳng x = 1 là tiệm cận đứng thì nghiệm kép của phương trình: x = 1

Do x = 1 là nghiệm của f(x) = x - 1 g(x) = 0 $\Leftrightarrow$

Vậy m + n = -4

Đăng ký ngay để nhận bí kíp nắm trọn kiến thức và phương pháp giải mọi dạng bài tập Toán thi THPT

2.4. Hàm số vô tỷ và tiệm cận

Dạng 4. Hàm số vô tỷ và tiệm cận

Phương pháp

Cho hàm số vô tỷ y = f(x1)

Tìm tập xác định N của hàm số.

Để có tiệm cận ngang của đồ thị hàm số y = f(x1) thì trong tập xác định N của hàm số phải chứa ít nhất một trong hai kí hiệu $- \infty$ hoặc $+ \infty$ và tồn tại ít nhất một trong hai giới hạn $\lim_{x\rightarrow -\infty } y$ hoặc $\lim_{x\rightarrow x^{+} } y$ hữu hạn.

Ví dụ 1: Biết đồ thị hàm số $y= 2x +\sqrt{ax^{2}+ bx+4}$ có tiệm cận ngang y = -1. Giá trị $2a +c^{3}$ bằng

A. 56

B. -56

C. -72

D. 72

Giải

Chọn B

ĐKXĐ ta có: ax² + bx + 4 ≥ 0

Để đồ thị hàm số có tiệm cận ngang thì ta phải có a > 0

Khi đó, ta có: $\lim_{x\rightarrow +\infty } y = \lim_{x\rightarrow +\infty } y (2x + \sqrt{ax^{2}+bx+4}) = + \infty$

Giải bài tập ví dụ toán 12 đường tiệm cận

Bài tập 2: Có bao nhiêu giá trị của tham số m để đồ thị hàm số $y= \frac{mx+ \sqrt{x^{2}-2+3}}{2x-1}$ có một đường tiệm cận ngang là y = 2?

A. 0

B. Vô số

C. 1

D. 2

Giải

Chọn D

Tập xác định D \ { $\frac{1}{2}$ }

Ta có $\lim_{x\rightarrow +\infty } y = \frac{m+1}{2} ; \lim_{x\rightarrow -\infty } y = \frac{m-1}{2}$ $\Leftrightarrow$ Giải bài tập ví dụ toán 12 đường tiệm cận

2.5. Biện luận đường tiệm cận của đồ thị hàm số chứa căn thức

Dạng 5: Hàm số y = f(x) có đồ thị, xác định tiệm cận của đồ thị hàm số $y= \frac{A1}{g(x)}$ với A là số thực khác 0, g(x) xác định theo f(x)

Phương pháp giải:

Xác định tiệm cận đứng:

Số tiệm cận của đồ thị hàm số $y= \frac{A1}{g(x)}$ là số nghiệm của phương trình g(x) = 0

Theo bảng biến thiên, đồ thị của hàm số y = f(x) để xác định số nghiệm của phương trình g(x) để suy ra số đường tiệm cận đứng.

Dựa vào nhánh vô tận của đồ thị xác định tiệm cận ngang, bảng biến thiên của hàm số để xác định.

Bài tập

Bài tập 1. Trên ℝ cho hàm số y = f(x1), bảng biến thiên bên dưới

Bảng biến thiên - toán 12 đường tiệm cận

Tổng số đường tiệm cận của hàm số $y= \frac{1}{f(x) +1}$

A. 2

B. 3

C. 1

D. 4

Giải

Chọn D

Số nghiệm của phương trình bằng số tiệm cận đứng: f(x) + 1 = 0 ⇔ f(x) = -1

Ta thấy phương trình có hai nghiệm phân biệt thông qua bảng biến thiên, vậy nên đồ thị hàm số $y= \frac{1}{f(x) +1}$ có hai đường tiệm cận đứng.

Ta có $\lim_{x\rightarrow +x}$ nên đồ thị hàm số có hai đường tiệm cận ngang là $y= \frac{1}{4} , y = \frac{1}{2}$

Vậy đồ thị hàm số $y= \frac{1}{f(x) +1}$ sẽ có 4 đường tiệm cận.

Bài tập 2: Xét y = f(x) xác định trên tập hợp các số thực

Bảng biến thiên - toán 12 đường tiệm cận

Hàm số $y= \frac{1}{(x^{3}+x)+3}$ là có tất cả số đường tiệm cận là bao nhiêu trong các đáp án sau:

A. 2

B. 4

C. 3

D. 1

Giải

Chọn A

Đặt k = x³+x, ta có khi x → $- \infty$ thì t → $- \infty$ và khi x → $+ \infty$ thì k→ $+ \infty$

Mặt khác ta có k’ = 3x2 + 1 > 0, ∀ x ∈ ℝ nên với mọi t ∈ ℝ phương trình x3 + x = k có duy nhất một nghiệm x.

Số nghiệm phương trình bằng số đường tiệm cận đứng

f(k) + 3 = 0 ⇔ f(k) = -3

Từ bảng biến thiên ta thấy phương trình có duy nhất một nghiệm nên đồ thị hàm số $y = \frac{1}{f (x^{3} +x)+3}$ có một tiệm cận đứng.

Ta có: $\lim_{x\rightarrow +\infty } \frac{1}{f (x^{3}+x)+3}= \lim_{x\rightarrow +\infty } \frac{1}{f(t)+3} = 0 ; \lim_{x\rightarrow -\infty } \frac{1}{f (x^{3}+x)+3}= \lim_{x\rightarrow -\infty }\frac{1}{f(t)+3} =0$ nên đồ thị hàm số $y= \frac{1}{(x^{3}+x)+3}$ có một tiệm cận ngang là y =0

Vậy đồ thị có hai đường tiệm cận.

2.6. Đồ thị hàm ẩn: biện luận

Dạng 6: Ta có đồ thị, bảng biến thiên của hàm số y = f(x),

Tiệm cận đồ thị hàm số $\frac{\varphi (x)1}{g(x)1}$ với φ(x) là một biểu thức theo x, g(x) là biểu thức theo f(x1)

Phương pháp giải

Theo hàm số y = f(x1) tìm nghiệm của phương trình g(x)1 = 0 và tìm biểu thức g(x)

Tìm tiệm cận đứng, tiệm cận ngang sau khi rút gọn biểu thức $\frac{\varphi (x)1}{g(x)1}$

Chú ý:

– Điều kiện tồn tại của φ(x)1

– Vận dụng tính chất nếu đa thức g(x) có nghiệm là x = x0 thì g(x)1 = (x – x0)․g1(x)1, ở đó g1(x)1 là một đa thức.

Bài tập

Bài tập 1.Ta có hàm số bậc ba f(x) = ax³ + bx³ + cx + d sau

Đồ thị ví dụ - toán 12 đường tiệm cận

Đồ thị hàm số $g(x) = \frac{x^{2}-3x+2 \sqrt{x-1}}{x|f^{2}(x)-f(x)}$ có số tiệm cận đứng là bao nhiêu trong các số sau:

A. 4

B. 6

C. 3

D. 5

Giải

Chọn C

Giải bài toán 12 đường tiệm cận

Bài tập 2. Có sẵn hàm số bậc ba f(x) = ax³ + bx² + cx + d có đồ thị như hình vẽ dưới đây.

Đồ thị ví dụ cho bài toán 12 đường tiệm cận

Đặt $g(x) = \frac{x^{2}-x}{f^{2}(x) -2f(x)}$ . Đồ thị hàm số y = g(x) có số tiệm cận đứng là?

A. 4

B. 2

C. 5

D. 3

Giải

Chọn A

Giải bài toán 12 đường tiệm cận

Bài giảng trong video dưới đây của thầy Thành Đức Trung sẽ hướng dẫn các em phương pháp tìm đường tiệm cận: tiệm cận đứng, tiệm cận ngang đây là 2 dạng sẽ xuất hiện trong đề thi đại học. Các em chú ý theo dõi bài học cùng thầy nhé!
Link đề tải TẠI ĐÂY

Đăng ký ngay để được các thầy cô tổng hợp kiến thức và xây dựng lộ trình ôn thi sớm ngay từ bây giờ

Trên đây là toàn bộ lý thuyết và các dạng bài trắc nghiệm của đường tiệm cận trong chương trình Toán 12. Tuy nhiên nếu em muốn đạt kết quả cao hơn thì hãy làm thêm nhiều dạng bài khác nữa. Ngoài ra, các em có thể truy cập Vuihoc.vn và đăng ký tài khoản để luyện đề! Chúc các em đạt kết quả cao trong kỳ thi tốt nghiệp THPT Quốc Gia môn Toán sắp tới.

>>Xem thêm bài viết:

Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Toán 12 - Phương pháp giải bài tập chương 1 và 2

Tìm tập nghiệm của phương trình logarit

Số phức liên hợp là gì? Tính chất và cách tìm chi tiết nhất

Hiểu rõ về cách giải phương trình logarit khác cơ số

Số phức nghịch đảo là gì? Lý thuyết và bài tập vận dụng

Cách Xét Tính Đơn Điệu Của Hàm Số Lượng Giác Và Bài Tập Trắc Nghiệm

| đánh giá

Toán 12 đường tiệm cận: Lý thuyết kèm bài tập trắc nghiệm

1. Lý thuyết đường tiệm cận - Toán 12

1.1. Đường tiệm cận ngang

1.2. Đường tiệm cận đứng

2. Các dạng toán 12 bài 4 đường tiệm cận kèm bài tập trắc nghiệm dễ hiểu nhất

2.1. Dựa vào định nghĩa để xác định các đường tiệm cận

2.2. Hàm số phân thức: tiệm cận của đồ thị

Phương pháp giải:

Ví dụ 1: Giá trị của tham số thực k để đồ thị hàm số có đường tiệm cận ngang y = 3 là:

Ví dụ 2: Tìm tập hợp giá trị thực của m để đồ thị có đường tiệm cận đứng là:

2.3. Dạng tiệm cận đồ thị của hàm số phân thức hữu tỉ

Dạng 3: Hàm số phân thức hữu tỉ và tiệm cận

Phương pháp giải:

Ví dụ 1: Tìm mọi giá trị thực tham số m thỏa mãn điều kiện đồ thị hàm số có tiệm cận đứng:

Ví dụ 2: Biết đồ thị hàm số (m, n là tham số) nhận đường thẳng x = 1 là tiệm cận đứng, giá trị của m + n bằng

2.4. Hàm số vô tỷ và tiệm cận

Phương pháp

Ví dụ 1: Biết đồ thị hàm số có tiệm cận ngang y = -1. Giá trị bằng

Bài tập 2: Có bao nhiêu giá trị của tham số m để đồ thị hàm số có một đường tiệm cận ngang là y = 2?

2.5. Biện luận đường tiệm cận của đồ thị hàm số chứa căn thức

Phương pháp giải:

Bài tập

Bài tập 1. Trên ℝ cho hàm số y = f(x1), bảng biến thiên bên dưới

2.6. Đồ thị hàm ẩn: biện luận

Phương pháp giải

Bài tập

Bài tập 1.Ta có hàm số bậc ba f(x) = ax3 + bx3 + cx + d sau

Bài tập 2. Có sẵn hàm số bậc ba f(x) = ax3 + bx2 + cx + d có đồ thị như hình vẽ dưới đây.

Ví dụ 1: Giá trị của tham số thực k để đồ thị hàm số $y= \frac{(2m+1) x+1}{x-m}$ có đường tiệm cận ngang y = 3 là:

Ví dụ 2: Tìm tập hợp giá trị thực của m để đồ thị $y= \frac{x-1}{mx-1}$ có đường tiệm cận đứng là:

Ví dụ 1: Tìm mọi giá trị thực tham số m thỏa mãn điều kiện đồ thị hàm số $y= \frac{mx^{2} -2x+1}{2x+1}$ có tiệm cận đứng:

Ví dụ 2: Biết đồ thị hàm số $y= \frac{x-1}{x^{2} -2mx+n+6}$ (m, n là tham số) nhận đường thẳng x = 1 là tiệm cận đứng, giá trị của m + n bằng

Ví dụ 1: Biết đồ thị hàm số $y= 2x +\sqrt{ax^{2}+ bx+4}$ có tiệm cận ngang y = -1. Giá trị $2a +c^{3}$ bằng

Bài tập 2: Có bao nhiêu giá trị của tham số m để đồ thị hàm số $y= \frac{mx+ \sqrt{x^{2}-2+3}}{2x-1}$ có một đường tiệm cận ngang là y = 2?

Bài tập 1.Ta có hàm số bậc ba f(x) = ax³ + bx³ + cx + d sau

Bài tập 2. Có sẵn hàm số bậc ba f(x) = ax³ + bx² + cx + d có đồ thị như hình vẽ dưới đây.